4.9. Princípy smerovacích algoritmov

Nastavenie smerovacej tabuľky môže byť buď statické alebo dynamické. Pri statickom smerovaní nastavuje smerovaciu tabuľku administrátor ručne. Nevýhoda tohto prístupu môže byť pri výpadkoch niektorých routrov v sieti, lebo ak by aj existovala alternatívna fungujúca cesta k cieľu, smerovanie by mohlo datagram poslať rovno smerom k nefunkčnému zariadeniu. Pri dynamickom smerovaní sa o nastavenie smerovacej tabuľky stará smerovací algoritmus niektorého z možných smerovacích protokolov.

Smerovacie algoritmy slúžia na zistenie aktuálne optimálnej cesty k všetkým dostupným sieťam a modifikáciu smerovacích tabuliek routrov tak, aby datagramy po svojej aktuálne optimálnej ceste k cieľu naozaj putovali.

Keďže routrov je na svete veľa, majú aj veľa správcov. Každý zo správcov má na starosti obvykle viacero sietí a routrov, ktoré tieto siete prepájajú. Takáto množina sietí sa nazýva autonómny systém (skrátene AS). Je na správcovi autonómneho systému, aby zvolil vhodný smerovací protokol vo svojom autonómnom systéme, ktorý sa bude starať o nastavovanie smerovacích tabuliek.

Stanica, vysielajúca datagram, je obvykle napojená k jedinému routru – predvolenej bráne, rovnako aj prijímajúca stanica. To znamená, že na koncových úsekoch cesty je smer putovania datagramu jednoznačný – priamo medzi stanicou a predvolenou bránou. V modeli siete budeme teda uvažovať iba routre (bez staníc), ktoré sú navzájom poprepájané pavučinou spojení. Na routre a spojenia medzi nimi sa môžeme pozerať ako na graf, kde routre sú vrcholy a spojenia sú hrany. Jednotlivé hrany môžu byť ohodnotené. Táto cena hrán môže byť interpretovaná ako čas potrebný na prenos datagramu medzi routrami, alebo aj ako miera zahltenia spojenia.

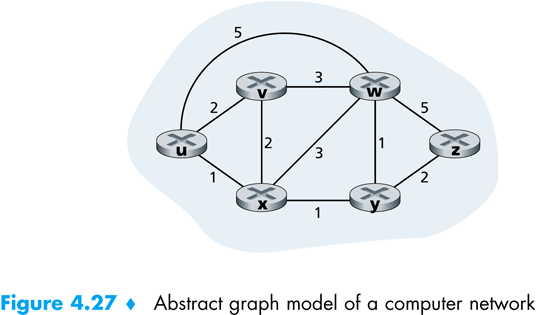
Uvažujme nasledujúci graf G = (V,E), kde V = {u, v, w, x, y, z} a E = (u, v), (u, x), (u, w), (v, x), (v, w), (x, w), (x, y), (w, y), (w, z), (y, z). Cenu hrany budeme označovať ako c(v₁, v₂), kde v₁ a v₂ sú vrcholy, napríklad cena c(w, z) = 5. Cena cesty (v₁, v₂, v₃, …, v_n,) = c(v₁, v₂) + c(v₂, v₃) + … + c(v_n-1, v_n).

Rozoznávame dva hlavné typy smerovacích algoritmov, ktoré sú základom pre konkrétne smerovacie protokoly vo vnútri autonómnych systémov. Prvým typom je LSA: link state algorithm, ktorý na svoj beh potrebuje poznať celú topológiu siete a ceny všetkých hrán. Ak tieto informácie má, vypočíta optimálne cesty ku všetkým routrom autonómneho systému. Druhý typ je DVA: distance vector algorithm. DVA nepotrebuje poznať celú topológiu siete, len ceny hrán fyzicky spojených s routrom, na ktorom tento algoritmus beží. Tiež je závislý na informáciách od svojich susedov, ktoré si spolu vymieňajú. DVA je iteratívny algoritmus, ktorý postupne konverguje k aktuálne optimálnym smerom pre jednotlivé cieľové routre.

4.9.1  LSA: link state algorithm

LSA je typ algoritmov, ktoré na svoj beh potrebujú poznať celú topológiu siete a ceny všetkých hrán. Táto informácia je obvykle šírená broadcastovými alebo multicastovými správami od všetkých routrov, pričom každý z routrov rozosiela správu o jeho lokálnych spojoch.

V reálnych protokoloch sa využíva Dijkstrov algoritmus, ktorý počíta najkratšie cesty z jedného uzla k všetkým ostatným. Keďže všetky uzly vedia celú topológiu, každý si vypočíta najkratšie cesty od seba k ostatným uzlom.

Dijkstrov algoritmus bol dôkladne preberaný v predmete PAZ1b, no v krátkosti si ho pripomenieme. Označíme D(v) ako aktuálne najmenšiu cenu cesty zo štartovacieho uzla do uzla v, ďalej označme p(v) ako predchodcu uzla v na aktuálne najkratšej ceste zo štartovacieho uzla a nakoniec označme N ako množinu uzlov, ku ktorým už poznáme definitívne najkratšiu cestu.

Inicializácia: N = {u}, kde u je štartovací uzol Pre všetkých susedov v uzla u nastav D(v) = c(u, v) a p(v) = u Pre všetky ostatné uzly w, ktoré nie sú susedom u nastav D(w)=∞ Výpočet: Pokiaľ N neobsahuje všetky uzly opakuj vezmi uzol w taký, že jeho D(w) je najmenšie zo všetkých uzlov, ktoré nie sú v N pridaj w do N vezmi každý uzol v, ktorý je susedom uzla w a ktorý zároveň nie je v N nastav D(v) = min{D(v), D(w) + c(w, v)} ak sa D(v) v predchádzajúcom kroku zmenilo, nastav p(v)=w

Ukážme si príklad použitia Dijkstrovho algoritmu. Predpokladajme, že chceme spustiť Dijkstrov algoritmus na vyššie znázornenom grafe v uzle u.

1. inicializácia
   • N={u}
   • D(u)=0, D(v)=2, D(w)=5, D(x)=1, D(y)=∞, D(z)=∞
   • p(u)=u, p(v)=u, p(w)=u, p(x)=u, p(y)=?, p(z)=?
2. Spomedzi vrcholov v, w, x, y, z, ktoré nie sú v N, si vyberieme uzol x, lebo má najmenšiu hodnotu vzdialenosti D(x). Vrchol x vložíme do N a prepočítame vzdialenosti pre všetkých susedov vrchola x, ktorí nie sú v N, teda vrcholov v,w a y.
   • N={u,x}
   • D(u)=0, D(v)=2, D(w)=4, D(x)=1, D(y)=2, D(z)=∞
   • p(u)=u, p(v)=u, p(w)=x, p(x)=u, p(y)=x, p(z)=?
3. Spomedzi vrcholov v, w, y, z ktoré nie sú v N, si vyberieme uzol y, lebo má najmenšiu hodnotu vzdialenosti D(y) (mohli by sme vybrať aj v). Vrchol y vložíme do N a prepočítame vzdialenosti pre všetkých susedov vrchola y, ktorí nie sú v N, teda vrcholov w a z.
   • N={u,x,y}
   • D(u)=0, D(v)=2, D(w)=3, D(x)=1, D(y)=2, D(z)=4
   • p(u)=u, p(v)=u, p(w)=y, p(x)=u, p(y)=x, p(z)=y
4. Spomedzi vrcholov v, w, z ktoré nie sú v N, si vyberieme uzol v, lebo má najmenšiu hodnotu vzdialenosti D(v). Vrchol v vložíme do N a prepočítame vzdialenosti pre všetkých susedov vrchola v, ktorí nie sú v N, teda vrchola w.
   • N={u,x,y,v}
   • D(u)=0, D(v)=2, D(w)=3, D(x)=1, D(y)=2, D(z)=4
   • p(u)=u, p(v)=u, p(w)=y, p(x)=u, p(y)=x, p(z)=y
5. Spomedzi vrcholov w, z ktoré nie sú v N, si vyberieme uzol w, lebo má najmenšiu hodnotu vzdialenosti D(w). Vrchol w vložíme do N a prepočítame vzdialenosti pre všetkých susedov vrchola w, ktorí nie sú v N, teda vrchola z.
   • N={u,x,y,v,w}
   • D(u)=0, D(v)=2, D(w)=3, D(x)=1, D(y)=2, D(z)=4
   • p(u)=u, p(v)=u, p(w)=y, p(x)=u, p(y)=x, p(z)=y
6. Už iba vložíme uzol z do N a môžeme skončiť.

Nakoniec pomocou údajov o predchodcoch uzlov vieme zrekonštruovať najkratšie cesty do všetkých uzlov v grafe. Z každej cesty si vezmeme iba prvý krok (v našom prípade buď do uzla v alebo do uzla x) a ten zapracujeme do smerovacej tabuľky.

cieľový router (cieľ)	susedný router na najkratšej ceste k cieľovému (brána)
v	v
w	x
x	x
y	x
z	x

Samozrejme do reálnej smerovacej tabuľky sa namiesto cieľových routrov zapíšu adresy sietí, ku ktorým majú tieto routre priamy prístup a namiesto „mena“ routra sa použije IP adresa rozhrania, ktoré je napojené na spoj s uzlom u.

Pri použití LSA môže v niektorým prípadoch dochádzať k osciláciám. Predstavme si situáciu, že za cenu hrany budeme považovať množstvo prenášaných dát za nejaký čas. Uvažujme jednoduchý graf so 4 vrcholmi. Vrcholy z a x vysielajú k vrcholu w konštantne 1 MB dát za sekundu a vrchol y vysiela k vrcholu w e MB dát za sekundu. Predpokladajme, že žiadna iná komunikácia v tomto grafe neprebieha.

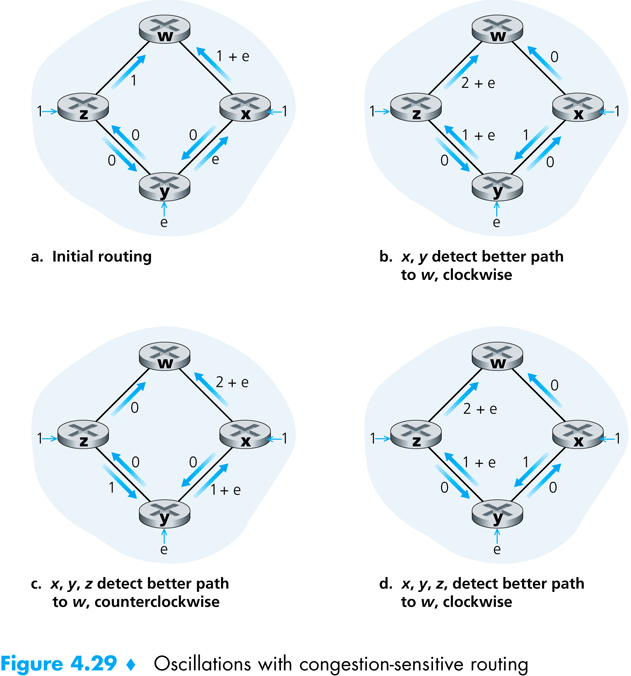
Ako môžeme vidieť na obrázku a, na začiatku boli smerovacie tabuľky uzlov nastavené tak, že datagramy zo z a x boli smerované priamymi spojmi k w a uzol y smeroval dáta pre w cez vrchol x. Keďže samotné posielanie dát zmenilo ceny hrán, je potrebné prepočítať smerovacie tabuľky. Pri prepočte zistia vrcholy x a y, že lacnejšia cesta k w je cez vrchol z a začnú smerovať datagramy týmto smerom. To ale opäť zmení ceny hrán a opäť sa začnú prepočítavať smerovacie tabuľky a vrcholy x, y aj z začnú smerovať datagramy opačným smerom a tak ďalej.

4.9.2  DVA: distance vector algorithm

DVA je algoritmus, ktorý pre každý uzol vychádza iba z cien susedných hrán a z informácií od svojich susedov. Každý vrchol si uchováva vektor podľa neho najlacnejších vzdialeností k všetkým vrcholom grafu a vektory vzdialeností svojich susedov, ktoré mu poslali.

DVA je založený na Bellman-Fordovej rovnici, ktorá vyjadruje vzťah medzi cenou najlacnejšej cesty z uzla x do uzla y a cenami ciest od susedov vrchola x do vrchola y. Označme d_x(y) ako cenu najlacnejšej cesty z uzla x do uzla y. Potom Bellman-Fordova rovnica hovorí, že:

d_x(y) = min_v {c(x,v) + d_v(y) }, cez všetky vrcholy v susedov vrchola x.

V algoritme DVA budeme používať označenie D_x(y) ako očakávanú najmenšiu cenu cesty z vrchola x do vrchola y. Každý vrchol si uchováva vektor vzdialeností ku všetkým vrcholom grafu, tento vektor označme D_x = [D_x(y): kde y je vrchol grafu]. Každý vrchol tiež pozná ceny s ním susediacich hrán a vektory vzdialeností svojich susedov.

Inicializácia v uzle u: Du(u)=0. Pre všetkých susedov v uzla u nastav Du(v) = c(u, v) a v ich vektoroch vzdialeností nastav vzdialenosti ku všetkým vrcholom na ∞ (lebo ich reálne vektory zatiaľ nemáme) Pre všetky ostatné uzly w, ktoré nie sú susedom u nastav Du(w)=∞ Pošli svoj vektor vzdialeností všetkým svojim susedom Ak príde vektor vzdialeností od niektorého suseda w, alebo ak sa zmenia ceny susedných hrán: Pre každý vrchol y nastav Du(y) = minv{c(u,v) + Dv(y) } Ak sa niekde zmenila hodnota z pôvodného vlastného vektora vzdialeností, pošli všetkým svojim susedom nový vektor vzdialenosti

Príklad výpočtu DVA na troch uzloch je znázornený na nasledujúcom obrázku. Na začiatku (ľavý stĺpec) sa všetky vrcholy a teda aj ich vektory vzdialeností inicializujú. Takáto inicializácia vo všetkých uzloch naraz je síce nepravdepodobná, ale pre účely vysvetlenia algoritmu si to môžeme dovoliť predpokladať.

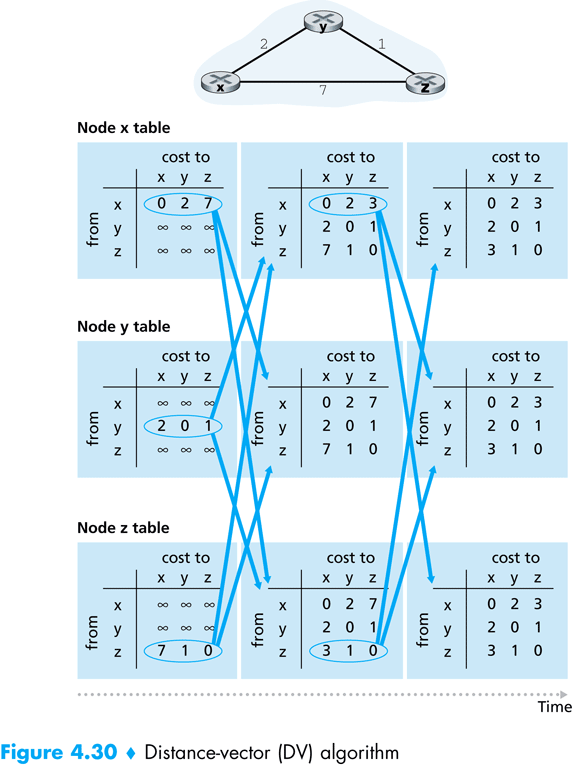
Po inicializácii pošlú všetky vrcholy svojim susedom svoje vektory vzdialeností. Vezmime si ako príklad vrchol x, ktorému prišli vektory D_y a D_z. Tieto vektory si uloží a ide prepočítať vlastný vektor podľa Bellman-Fordovej rovnice. Prepočítame D_x(y) a D_x(z):

D_x(y) = min {c(x,y) + D_y(y) ,c(x,z) + D_z(y)} = min{2+0, 7+1} = 2
D_x(z) = min {c(x,y) + D_y(z) ,c(x,z) + D_z(z)} = min{2+1, 7+0} = 3

Keďže sa nám zmenila hodnota D_x(z), zmenil sa aj celý vektor a musíme ho poslať svojim susedom. Okrem toho si vrchol x zapíše do smerovacej tabuľky, že datagramy pre vrcholy y aj z má posielať cez vrchol y. Podobne sa zmenil aj vektor vzdialeností vrchola z. Vektor vrchola y sa nezmenil, takže ten svoj už vektor neposiela. V ďalšej fáze si opäť všetky tri vrcholy prepočítajú svoje vektory vzdialeností, a keďže žiadnemu sa jeho vektor nezmení, žiadne ďalšie vektory sa neposielajú a systém ostane stabilný.

Pri zmene ceny niektorej hrany na to zareagujú susedné routre a prepočítajú svoje vektory vzdialeností. Ak dôjde k zmene vektora, zasielajú ho svojim susedom, tí si prepočítajú svoje vektory a tak sa táto informácia môže šíriť ďalej. Predstavme si situáciu na nasledujúcom obrázku.

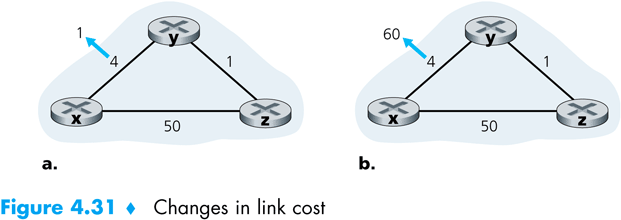
Prvý prípad vykresľuje situáciu, keď sa cena hrany (x,y) zmení zo 4 na 1. V tomto prípade si vrcholy x a y prepočítajú svoje vektory vzdialeností. Všimnime si, ako sa zmení vektor vrchola y. Pôvodný vektor (4,0,1) sa zmení na (1,0,1). Tento vektor pošle susedom. Čo sa stane vo vrchole z? Pôvodný vektor vrchola z (5,1,0) sa zmení na (2,1,0). Tento vektor pošle svojim susedom, ale u nich sa už po prepočítaní vektory vzdialeností nezmenia a systém sa stabilizuje.

V druhom prípade sa zmení cena hrany (x,y) zmení zo 4 na 60. Čo sa stane? Na začiatku má vrchol y vektor vzdialeností (4,0,1) a z má vektor (5,1,0). Po zmene ceny hrany si y prepočíta svoj vektor podľa Bellman-Fordovej rovnice (min{60+0, 1+5} = 6, 0, 1) a pošle ho susedom. Vrchol z si následne prepočíta svoj vektor (min{50+0, 1+6} = 7, 0, 1) a pošle ho susedom. Vrchol y si následne prepočíta svoj vektor (min{60+0, 1+7} = 8, 0, 1) a tak ďalej. Takéto posielanie sa vykoná celkovo 44 krát, kým dôjde k stabilizácii. Hovoríme o takzvanom count to infinity probléme, teda o „počítaní do nekonečna“. Tomuto problému sa v stromových sieťach dá vyhnúť technikou „poisoned reverse“, kde sa pri odhalení počítania do nekonečna môže jeden z uzlov rozhodnúť zmeniť hodnotu vo svojom vektore jedenkrát na nekonečno a potom opäť hlásiť reálne hodnoty vektora, lebo ako sme videli pri znižovaní cien, sa zmeny prejavia rýchlo. „Poisoned reverse“ však stráca svoju silu v sieťach s cyklami, kde je veľmi náročné odhaliť stav počítania do nekonečna.

Výber toho, či použiť protokol založený na LSA alebo na DVA je na administrátorovi siete. Oba prístupy majú svoje výhody aj nevýhody. LSA vyžaduje pri každej zmene výmenu všetkých informácii v sieti broadcastovými alebo multicastovými správami od všetkých routrov. DVA posiela správy iba medzi susedmi, ale zato možno aj niekoľko, či až veľmi veľakrát (count to infinity problém). LSA na druhej strane môže spôsobiť oscilácie. Dijkstrov algoritmus vyžaduje čas O(e log(n)), kde n je počet vrcholov a e je počet hrán. DVA prepočíta vektor v čase O(n), ale urobí to potenciálne aj veľakrát, kým sa stabilizuje.