Odhaľovanie chýb slúži na to, aby si príjemca bol primerane istý tým, že dostal presne tie isté dáta, ktoré boli odoslané odosielateľom. Za chybu sa typicky považuje výmena nejakých bitov na opačné. Chyby sú spôsobované rôznymi vplyvmi externého prostredia na fyzický spoj.
Kontrola je umožnená tak, že sa k odosielaným dátam pribalia ďalšie tzv. kontrolné bity. Chyba môže nastať v pôvodných dátach, ale aj v kontrolných bitoch. Odhalenie všetkých druhov chýb nie je vo všeobecnosti stopercentné. Čím viac je kontrolných bitov, tým je väčšia šanca na odhalenie prípadnej chyby. Samozrejme závisí aj na spôsobe, akým sa samotná kontrola realizuje. Ukážeme si tri spôsoby kontroly chýb: kontrola parity, kontrolný súčet a CRC.
5.2.1 Kontrola parity
Kontrola parity je najjednoduchšie realizovateľná kontrola dát. Pri základnej kontrole parity pridávame k dátam iba jeden kontrolný bit, tzv. paritný bit. Jeho hodnotu určíme tak, že spočítame počet jednotiek v binárnej reprezentácii dát. Ak je tento počet párny, paritný bit má hodnotu nula a ak je nepárny, tak paritný bit má hodnotu jedna. Ak sa v takto odoslaných dátach zmení nepárny počet bitov, tak príjemca odhalí chybu. Úspešnosť tejto metódy je teda 50 %.
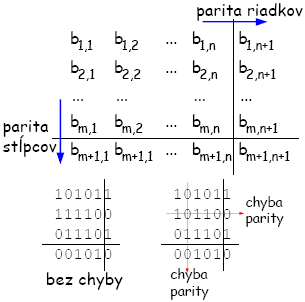
Špeciálny spôsob kontroly parity je bloková kontrola parity. Pri tomto spôsobe rozdelíme dáta na m blokov po n bitoch. Najprv vypočítame paritu každého bloku a paritný bit zapíšeme na koniec bloku ako (n + 1)-vý bit bloku. Nakoniec vypočítame parity i-tých bitov zo všetkých blokov pre i z intervalu <1,n+1>. Získame tak n+m+1 paritných informácií, ktoré sa pribalia k pôvodným dátam ako kontrolné bity. Ak sa pri prenose vyskytne chyba iba v jednom bite, príjemca je schopný túto chybu opraviť, pretože je schopný identifikovať presné miesto, kde chyba nastala. Ak vie príjemca chybu opraviť, nie je potrebné žiadať o opätovné zaslanie dát. Ak sa vyskytne viac chýb, tak oprava pri tomto spôsobe už možná nie je. Na druhej strane má tento spôsob vyššiu šancu odhaliť chyby ako jediný paritný bit. Úspešnosť je zhruba 70 – 80%.
5.2.2 Kontrolný súčet
Kontrolný súčet sme už vysvetľovali na 4. prednáške. Tento spôsob kontroly sa využíva v transportnej vrstve. Kontrolný súčet je náročné počítať hardvérovou implementáciou, je určený skôr na softvérové spracovanie. Úspešnosť tejto metódy je vyše 95 percentná.
5.2.3 CRC : kontrola cyklickým polynómom
CRC (cyclic redundancy check) je metóda, ktorá má hneď dve výhody. Prvou je ľahká hardvérová implementácia a druhou je vysoká úspešnosť odhaľovania chýb – až 99,99999998 % chýb rámcov pri použití 32 kontrolných bitov.
Aj keď hardvérová implementácia je jednoduchá, na jej pochopenie je potrebné poznať aj matematické pozadie tejto metódy. Najprv si povedzme, čo je to cyklický polynóm. Cyklický polynóm s koeficientami zo zvyškovej triedy modulo m, je taký polynóm, ktorého koeficienty môžu mať hodnoty iba celé čísla z intervalu <0,m-1>. V metóde CRC používame cyklické polynómy s koeficientami zo zvyškovej triedy modulo 2. To znamená, že koeficientami polynómu môžu byť iba čísla 0 alebo 1. Pre jednoduchosť už budeme namiesto cyklického polynómu s koeficientami zo zvyškovej triedy modulo 2 hovoriť iba cyklický polynóm.
Na dáta D sa budeme pozerať ako na koeficienty cyklického polynómu D(x).
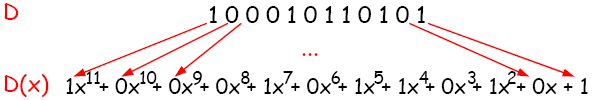
Odosielateľ aj príjemca musia mať vopred dohodnutý kontrolný cyklický polynóm G(x) stupňa r. Kontrolné polynómy sú určené príslušnými normami pre jednotlivé protokoly. Napríklad v Ethernete sa používa štandardizovaný cyklický polynóm stupňa 32: x32+x26+x23+x22+x16+x12+x11+x10+x8+x7+x5+x4+x2+x+1.
Pre účely vysvetlenia fungovania CRC predpokladajme kontrolný cyklický polynóm stupňa 3: x3+x+1.
Ako prvý krok výpočtu vynásobíme dátový polynóm D(x) s xr teda v tomto prípade s x3. Predpokladajme, že naše dáta D sú 10101. D(X) je potom x4+x2+1. Ten v prvom kroku vynásobíme s x3 a dostaneme tak cyklický polynóm x7+x5+x3.
V druhom kroku tento polynóm vydelíme kontrolným polynómom x3+x+1. Pri výpočte nás nezaujíma výsledok delenia, ale zvyšok po delení. Koeficienty zvyšku po delení tvoria kontrolnú informáciu, ktorá sa prikladá k odosielaným dátam. Znázornime si, ako by prebiehal na papieri výpočet delenia týchto cyklických polynómov.
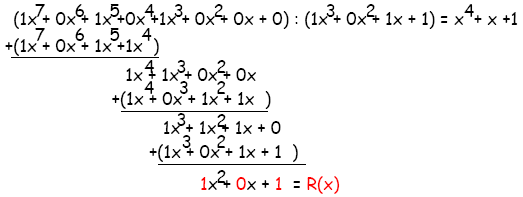
V prvom kroku sme vynásobili kontrolný polynóm (deliteľ) s x4, čím sme dostali polynóm x7+x5+x4. Ten sme odčítali od delenca a vyšiel nám zvyšok x4+x3. Ten sa stále dá deliť kontrolným polynómom, takže sme vynásobili kontrolný polynóm s x, čím sme dostali polynóm x4+x2+x. Ten sme odčítali od x4+x3 a vyšiel nám zvyšok x3+x2+x. Ten sa stále dá deliť kontrolným polynómom, takže sme vynásobili kontrolný polynóm s 1, čím sme dostali polynóm x3+x+1. Ten sme odčítali od x3+x2+x a vyšiel nám zvyšok x2+1. Ten sa už ďalej deliť kontrolným polynómom nedá, takže máme konečný zvyšok po delení reprezentovaný polynómom R(x). Ak z neho extrahujeme iba koeficienty, dostaneme kontrolné bity R s hodnotami 101, ktoré sa majú pripojiť za dáta.
V tomto príklade sme používali operáciu odčítania. Táto operácia je v prípade cyklických polynómov identická s operáciou sčítania a s operáciou XOR, pretože koeficienty polynómov sú zo zvyškovej triedy modulo 2. V tejto zvyškovej triede teda platí:
| 0 + 0 = 0 | 0 – 0 = 0 | 0 XOR 0 = 0 |
| 0 + 1 = 1 | 0 – 1 = 1 | 0 XOR 1 = 1 |
| 1 + 0 = 1 | 1 – 0 = 1 | 1 XOR 0 = 1 |
| 1 + 1 = 0 | 1 – 1 = 0 | 1 XOR 1 = 0 |
Keďže pri delení násobíme kontrolný polynóm vždy len s nejakým 1xk, výsledný polynóm, ktorý ideme odčítavať od predchádzajúceho zvyšku, má až na rád mocnín stále rovnaký tvar. V prípade nášho kontrolného polynómu x3+x+1, čo je to isté ako 1x3+0x2+1x1+1x0, je to 1x3+k+0x2+k+1x1+k+1x0+k. Ak si vypíšeme iba koeficienty dostávame číslo 1011, za ktorým nasleduje k núl. Napríklad v prvom kroku delenia sme násobili kontrolný polynóm s x4, teda koeficienty, ktoré dostávame sú 10110000. Toto pozorovanie využijeme.
Zjednodušme si teraz celý zápis výpočtu iba na koeficienty, teda na pôvodné binárne dáta, ktoré chceme preniesť. Namiesto sčítavania/odčítavania budeme písať XOR, lebo je to prirodzenejšie pre binárne zápisy čísiel.
10101000 : 1011 = výsledok nás nezaujíma
XOR 1011
----
0001100
XOR 1011
----
01110
XOR 1011
----
101
Vidíme, že koeficienty kontrolného polynómu 1011, sme použili na operáciu XOR vždy so zarovnaním na prvú jednotku predchádzajúceho zvyšku. V tomto prípade to znamená, že na začiatku si číslo 1011 (za ním si predstavíme 4 nuly) napíšeme pod číslo 10101000 so zarovnaním doľava a urobíme XOR. Výsledkom je 00011000. Keď si odmyslíme prvé tri nuly tak máme zvyšok 11000. Pod neho si zapíšeme známe číslo 1011 so zarovnaním doľava (za ním si predstavíme ešte jednu nulu) a vypočítame XOR. Výsledok je 01110. Urobíme ešte jeden XOR s číslom 1011. Výsledok 101 je už kratší ako 1011 a môžeme skončiť. Nakoniec sme dostali zvyšok 101, ako v predchádzajúcom výpočte. Odosielame dáta 10101 spolu so zvyškom 101, teda 10101101.
Čo s tým spraví príjemca? Vezme doručenú postupnosť 10101101, pozrie sa na ňu ako na cyklický polynóm x7+x5+x3+x2+1 a ten vydelí vopred dohodnutým kontrolným cyklickým polynómom G(x)=x3+x+1. Ak je zvyšok po tomto delení nula, považujeme postupnosť s veľkou pravdepodobnosťou za neporušenú . Naopak, ak zvyšok po delení nie je nula, odhalili sme chybu. Napíšme si už rovno výpočet v zjednodušenej forme iba s koeficientmi.
10101101 : 1011 = výsledok nás nezaujíma
XOR 1011
----
0001110
XOR 1011
----
01011
XOR 1011
----
0000
Ako vidíme, výpočet „na papieri“ je vcelku jednoduchý. Reálne sa ale výpočet realizuje inak, aby bol výpočet rýchly a hlavne jednoducho hardvérovo realizovateľný. Pri návrhu „výpočtového“ obvodu sa vychádza z kontrolného cyklického polynómu. Samotný obvod sa skladá iba z posuvných registrov a XOR hradiel. Ak používame kontrolný cyklický polynóm stupňa r, zapojíme vedľa seba r posuvných 1 bitových registrov a všade tam, kde sa nachádza koeficient 1 ešte vložíme XOR hradlo okrem jednotky pri xr. Pre náš kontrolný cyklický polynóm G(x)=x3+x+1 by tento obvod vyzeral nasledovne:
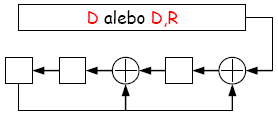
Po spracovaní celého vstupu je v registroch výsledný zvyšok po delení. Pekné animácie o tom, ako výpočet prebieha môžete nájsť napríklad na wikipedii.
